The computational design process in engineering often begins with a problem or goal, followed by an assessment of the literature, resources, and systems available to solve the problem. Instead, the Design Computation and Digital Engineering (DeCoDE) lab at MIT is exploring the limits of what’s possible.
In collaboration with the MIT-IBM Watson AI Lab, group leader ABS Career Development Assistant Professor Faez Ahmed and graduate student Amin Heyrani Nobari in the Department of Mechanical Engineering combine machine learning and generative artificial intelligence techniques, physical modeling, and engineering principles. tackle design challenges and improve the creation of mechanical systems. One of their projects, Bindingsexplore the ways in which plane bars and joints can be connected to curved paths. Here, Ahmed and Nobari describe their recent work.
Q: How does your team consider approaching mechanical engineering questions from an observational perspective?
Ahmed: The question we have been thinking about is: How can generative artificial intelligence be used in engineering applications? A key challenge is incorporating accuracy into generative AI models. Now, in the specific work that we’ve explored there, we’re using this idea of contrastive, self-supervised learning approaches where we’re effectively learning these linkages and curvilinear representations of design or what design looks like and how it works.
This is very closely related to the idea of automatic discovery: Can we really discover new products with AI algorithms? Another comment on the bigger picture: one of the key ideas, specifically with bindings, but broadly around generative artificial intelligence and large language models – it’s all the same family of models that we’re looking at, and accuracy plays a really big role. all of them. So the insights that we have from these types of models, where you have some form of data-driven learning with engineering simulators and collaborative design embeddings, and performance — can potentially transfer to other engineering domains as well. What we are showing is a proof of concept. Then people can take that and design ships and planes and exact image generation problems and so on.
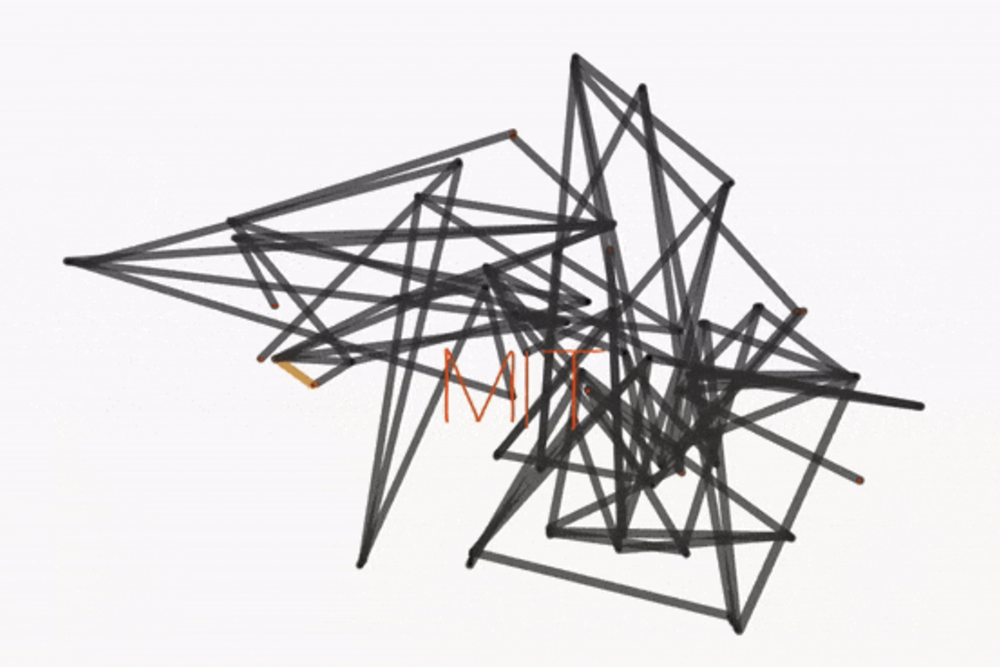
For joints, your design looks like a set of rods and how they are connected. The way it works is basically the path they would rewrite as they moved, and we learn these joint representations. So here’s your primary input—someone comes along and draws some path—and you’re trying to create a mechanism that can trace it. This allows us to solve the problem in a much more accurate way and significantly faster, with 28 times less error (more accurate) and 20 times faster than previous state-of-the-art approaches.
Q: Tell me about the linking method and how it compares to other similar methods.
Nobari: Contrastive learning happens between mechanisms that are represented as graphs, so basically each link will be a node in the graph and the node will contain some functions. Properties are position, space and type of joints, it can be fixed or loose joints.
We have an architecture that takes some basic fundamentals into account when it comes to describing the kinematics of a mechanism, but it’s essentially a graph neural network that computes the embeddings for these mechanism graphs. Then we have another model that takes these curves as inputs and creates an embedding for them, and we combine these two different modalities using contrastive learning.
Then this contrast learning framework that we train is used to find new mechanisms, but of course we also care about accuracy. In addition to all identified candidate mechanisms, we also have an additional optimization step where these identified mechanisms will be further optimized to get as close as possible to these target curves.
If you’ve got the combinatorial part right and you’re pretty close to where you need to be to get to the target curve you have, you can do direct optimization based on the gradient and adjust the position of the joints to get super accurate performance on it. This is a very important aspect of functioning.
These are examples of letters of the alphabet, but they are very difficult to achieve traditionally using existing methods. Other machine learning-based methods often aren’t even capable of this kind of thing because they’re only trained on four or six measures, which are very small mechanisms. But what we were able to show is that even with a relatively small number of joints, you can get very close to these curves.
Before that, we didn’t know what the limits of design possibilities were with a single coupling mechanism. It is very difficult to know. You really can write the letter M, can’t you? No one has ever done it, and the mechanism is so complex and so rare that it’s looking for a needle in a haystack. But with this method we show that it is possible.
We investigated the use of common generative models for graphs. In general, generative models for graphs are very difficult to train and usually not very efficient, especially when mixing continuous variables, which have a very high sensitivity to what the actual kinematics of the mechanism will be. At the same time, you have all these different ways of combining joints and connections. These models simply cannot generate effectively.
I think the complexity of the problem is more apparent when you look at how people approach it with optimization. With optimization, this becomes a nonlinear mixed-integer problem. Using some simple two-level optimizations, or even simplifying the problem down, they essentially create approximations of all the functions so they can use mixed-integer conic programming to approach the problem. The combinatorial space combined with the continuous space is so large that up to seven connections can basically fit. In addition, it is extremely difficult, and it takes two days to create one mechanism for one specific target. If you did this exhaustively, it would be very difficult to really cover the entire design space. This is where you can’t just learn more deeply without trying to be a little smarter about how you do it.
State-of-the-art deep learning approaches use reinforcement learning. These mechanisms will start to build more or less randomly – given the target curve, essentially a Monte Carlo optimization approach. The benchmark for this is a direct comparison of the curve that the mechanism follows and the target curves that are input to the model, and we show that our model performs about 28 times better. It is 75 seconds for our approach and 45 minutes for the reinforcement learning approach. An optimization approach, you run it for more than 24 hours and it doesn’t converge.
I think we’ve reached a point where we have a very robust proof of concept with linkage mechanisms. It is such a complicated problem that we can see that conventional optimization and conventional deep learning alone are not enough.
Q: What is the bigger picture behind the need to develop techniques such as interconnects that enable future human-AI co-design?
Ahmed: The most obvious is the construction of machines and mechanical systems, which we have already shown. Still, I think the key benefit of this work is that it is a discrete and continuous space in which we learn. So if you think about the connections that are out there and how the connections are connected to each other, it’s a discrete space. You’re either connected or you’re not: 0 and 1, but where each node is is a continuous space that can change – you can be anywhere in space. Learning these discrete and continuous spaces is an extremely challenging problem. Most of the machine learning we see, like in computer vision, is just continuous or the language is mostly discrete. By showing this discrete and continuous system, I believe the key idea generalizes to many engineering applications from metamaterials to complex networks, other types of structures, and so on.
There are steps that we immediately think about, and the natural question is about more complex mechanical systems and more physics, like when you start adding different forms of elastic behavior. Then you can also think about different types of components. We are also thinking about how to incorporate accuracy in large language models and transfer some of the insights there. We think about making these models generative. Right now, in a sense, they’re getting the mechanisms and then optimizing them from a dataset, while generative models will generate those methods. We also investigate complex learning where no optimization is needed.
Nobari: There are several places in engineering where these are used, and there are very common applications of systems for this kind of inverse kinematic synthesis where it would be useful. A few that come into play are for example in automotive suspension systems where you want a specific path of movement for your overall suspension mechanism. They usually model it in 2D using planning models of the overall suspension mechanism.
I think the next step, and what will ultimately be very useful, is to demonstrate the same or a similar framework for other complicated problems that involve combinational and continuous values.
These issues involve one of the things I’ve been researching: compliance mechanisms. For example, when you have the mechanics of continuous – instead of these discrete – solid links, you would have a distribution of materials and movement, and one part of the material deforms the rest of the material to give you a different kind of movement.
With compliant mechanisms, there are a lot of different places where they are used, sometimes in precision machinery for clamping mechanisms, where you want a specific piece held in place by a mechanism that clamps it, which can do this consistently and with very high accuracy. If you could automate this with this kind of framework, it would be very helpful.
These are all complex problems involving both combinatorial design variables and continuous design variables. I think we are very close to it and eventually it will be the final stage.
This work was supported in part by the MIT-IBM Watson AI Lab.